简介

MVME340  当电源设计人员想要大致了解电源的反馈环路时，他们会利用环路增益和相位波特图。知道环路响应可进行预测有助于缩小反馈环路补偿元件的选择范围。生成增益和相位图的精准方法是：在试验台上连接电源，并使用网络分析仪；但在设计的早期阶段，大部分设计人员会选择采用计算机模拟，通过模拟快速确定大致的元件选择范围，并且，更直观地了解环路对参数变化的响应。

本文主要研究适用于电流模式控制电源的反馈控制模型。电流模式控制在开关模式DC-DC转换器和控制器中相当常见，相比电压模式控制，它具有多项优势：更出色的线路噪声抑制、自动过流保护、更易于进行并联操作，以及得到改善的动态响应。

设计人员已经可以采用大量电流模式电源平均模型。有些模型的精准度达到开关频率的一半，可以匹配不断增高的转换器带宽，但只适用于有限的拓扑，例如降压、升压，以及降压-升压拓扑（非4开关降压-升压）。遗憾的是，适用于SEPIC和?uk等拓扑的3端口或4端口平均模型的精准度还达不到开关频率的一半。

本文将介绍LTspice®模拟模型，其精准度达到开关频率（甚至是相对较高的频率）的一半，适合多种拓扑，包括：

1. 降压
2. 升压
3. 降压-升压
4. SEPIC
5. ?uk
6. 正激式
7. 反激式

本文展示分段线性系统(SIMPLIS)结果模拟，以确定新模型的有效性，并举例说明模型的具体应用。在一些示例中，使用测试结果来验证模型。

电流模式控制模型：简要概述

MVME340  在这部分，我们将重申关于电流模式控制模型的一些要点。为了更全面地了解电流模式模型，请参阅文末“参考资料”部分中提到的刊物。

电流环路的作用在于：让电感电流循着控制信号的路线行进。在电流环路中，平均电感电流信息被反馈给具有检测增益的调制器。调制器增益Fm可通过几何计算得出，前提是，假设恒定电感电流斜坡上升，外部补偿电流也斜坡上升。为了模拟电感电流斜坡上升变化的影响，我们在模型中额外增加了两个增益：前馈增益(kf)和反馈增益(kr)，如图1所示。

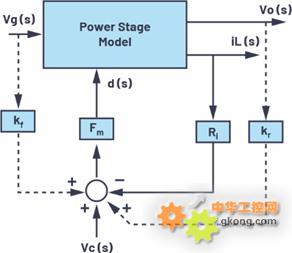
图1.电流模式控制的平均模型，绘图：R. D. Middlebrook

为了将图1所示的平均模型的有效性扩展到高频范围，研究人员基于离散时间分析和样本数据分析的结果，提出了几种经过改进的平均模型。在R. B. Ridley的模型（参见图2）中，采样保持效应可以用He(s)函数等效表示，它可以插入连续平均模型的电感电流反馈路径中。由于该模型是从离散时间模型演化而来，所以能够准确预测次谐波振荡。

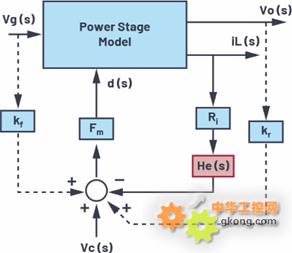
图2.经过改进的电流模式控制的平均模型，绘图：R. B. Ridley

另一种经过改进的平均模型由F. D. Tan和R. D. Middlebrook提出。为了考虑电流环路中的采样效应，必须在源自低频模型的电流环路增益上再增加一个极点，如图3所示。

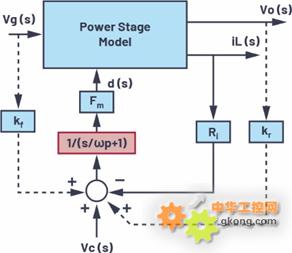
图3.经过改进的电流模式控制的平均模型，绘图：F. D. Tan

除了R. B. Ridley的模型外，R. W. Erickson提出的电流控制模型也很受欢迎。电感电流波形如图4所示。

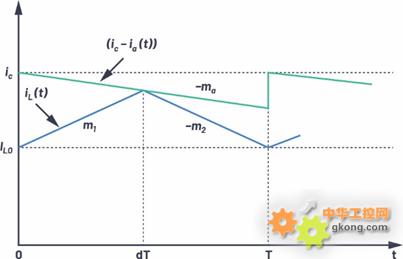
图4.稳态电感电流波形，包含外部补偿斜坡上升

平均电感电流表示为：

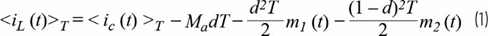
其中iL表示检测到的电流，ic表示误差放大器发出的电流命令，Ma表示外加补偿斜坡，m1和m2分别表示输出电感电流的上升和下降斜坡。扰动和线性化结果：

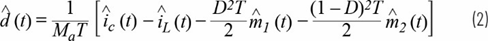
MVME340 根据此公式和规范开关模型，可以得出电流模式转换器模型。

一个经过改进的新平均模型

R. W. Erickson的模型可以帮助电源设计人员从物理角度深入了解，但其精准度还不到开关频率的一半。为了将该模型的有效性扩展到高频范围，我们基于离散时间分析和样本数据分析的结果，提出了一种经过改进的平均模型（参见图5）。

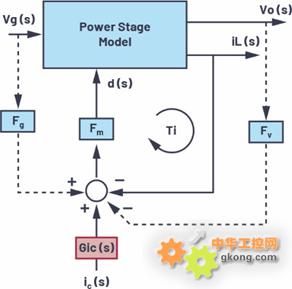
图5.提出的经过改进的电流模式控制平均模型

根据电感动态采样数据模型，可以得出：

其中，T为开关周期，

可以得出图5所示的模型的Gic(s)：

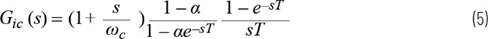
MVME340  其中ωc是内部电流环路Ti的穿越频率，如图5所示，关于各种拓扑的值ωc，请参见表1。

表1.不同拓扑的内部电流环路交叉频率(ωc)

*对于两个单独的电感，L=L1×L2/(L1+L2)

**NSP是次级与初级的匝数比

降压转换器示例

在图5中，我们将Fv反馈环路与iL反馈环路并联。我们也可以将Fv反馈环路作为iL反馈环路的内部环路。图6显示了包含附加的Gic(s)级的完整降压转换器模型。

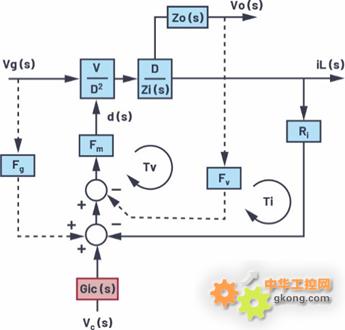
图6.经过改进的降压转换器平均模型的框图

控制至输出传递函数Gvc (s)为

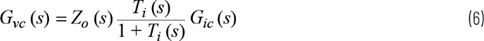
电流环路增益Ti (s)和电压环路增益Tv (s)可以通过以下公式计算得出：

和

其中：

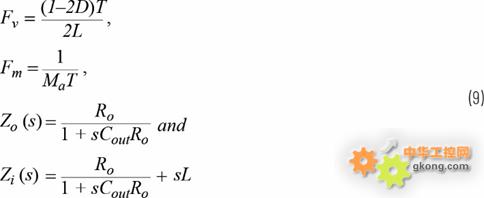
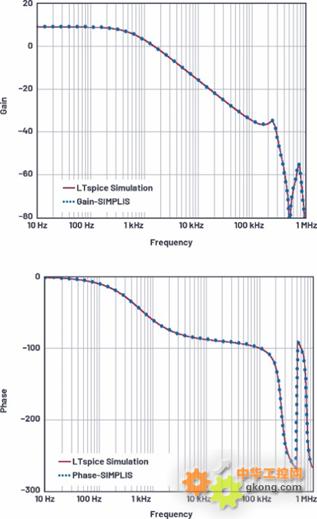
在图7中，基于新电流模式模型计算得出的环路增益与SIMPLIS结果一致。在这个示例中，VIN = 12 V，VOUT = 6 V，IOUT = 3 A，L = 10 µH，COUT = 100 µF，fSW = 500 kHz。